Perbandingan Trigonometri Segitiga Siku Siku

 Silviany Puteri Aulia

X IPS 2 ABSEN 32

Contoh Soal Perbandingan Trigonometri Segitiga Siku Siku

Apa pengertian perbandingan trigonometri itu? Perbandingan trigonometri merupakan perbandingan dalam segitiga siku siku antara ukuran sisi dengan sudut di dalamnya. Materi perbandingan trigonometri tersebut dapat diselesaikan dengan rumus tertentu. Salah satunya ialah rumus pada segitiga siku siku yang memuat beberapa jenis sisi di dalamnya seperti sisi depan sudut, sisi miring dan sisi depan.

Kemudian dalam bangun segitiga ini sering menggunakan konsep teorema phytagoras di dalamnya. Akan tetapi dalam panjang segitiga siku siku biasanya mengandung jenis jenis perbandingan trigonometri seperti sinus, secan, cosinus, cosecan, tangen dan cotangen. Untuk lebih jelasnya perhatikan segitiga berikut:

Baca juga : Contoh Soal Kesebangunan Segitiga dan Jawabannya

Gambar Segitiga Siku Siku

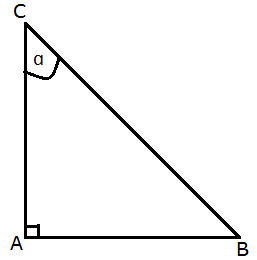
Dalam gambar di atas terdapat segitiga ABC yang memiliki siku siku di A. Untuk itu akan diperoleh rumus perbandingan trigonometri seperti di bawah ini: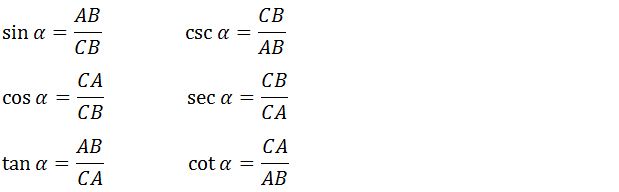

Dalam materi perbandingan trigonometri memang memuat sisi segitiga yang berhubungan dengan sudut sudut segitiganya. Untuk itu rumus persamaan yang digunakan berasal dari rumus segitiga dan rumus lainnya. Di bawah ini terdapat contoh soal perbandingan trigonometri pada segitiga siku siku. Berikut contoh soal dan pembahasannya:

1. Perhatikan gambar berikut!

Tentukan besar sudut yang sesuai dengan gambar di atas?

Pembahasan.
Pada umumnya sudut yang terbentuk berdasarkan gambar di atas menggunakan arah jarum jam. Maka dari itu sudut tersebut memiliki tanda negatif sehingga besarnya -30°. Kemudian dalam besar sudut satu putaran penuh biasanya memiliki nilai 360°. Sehingga sudut yang sesuai gambar di atas besarnya menjadi:
360° – 30° = 330°
Jadi besar yang sesuai dengan gambar tersebut ialah 330°.

2. Tentukan besar sudut ¼ π rad dalam bentuk derajat?

Pembahasan.
Contoh soal perbandingan trigonometri ini dapat diselesaikan dengan cara seperti berikut:
1 π rad = 180°

Maka,
¼ π rad = ¼ x 180° = 45°
Jadi besar ¼ π rad ialah 45°.

Baca juga : Rumus Sudut Pusat Lingkaran dan Sudut Keliling Lingkaran

3. Tentukan besar sudut 60º dalam bentuk rad?

Pembahasan.
1º = π/180 rad
60º = 60 x π/180 rad
      = 1/3 π rad
Jadi besar sudut 60º ialah 1/3 π rad.

4. Perhatikan gambar berikut!

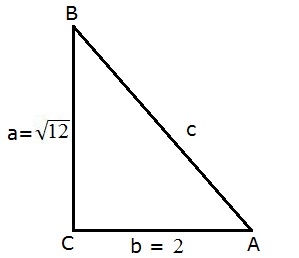
Hitunglah nilai cos α pada segitiga tersebut?

Pembahasan.
Contoh soal perbandingan trigonometri tersebut dapat diselesaikan dengan mencari nilai c terlebih dahulu. Nilai c tersebut dapat ditentukan menggunakan konsep teorema phytagoras seperti di bawah ini:
c² = a² + b²
    = (√12)² + 2²
    = 12 + 4
 c = √16
    = 4 

Maka,
cos α = b/c  (Sisi Samping / Sisi Miring)
         = 2/4
         = ½
Jadi nilai cos α pada segitiga tersebut ialah ½.